О суммах квадратов и кубов
История, о которой пойдёт речь, начинается с теоремы Пифагора, а заканчивается одним математическим открытием, сделанным в сентябре 2019 года. Точнее сказать, эта история ещё не окончена…
Пифагоровы тройки
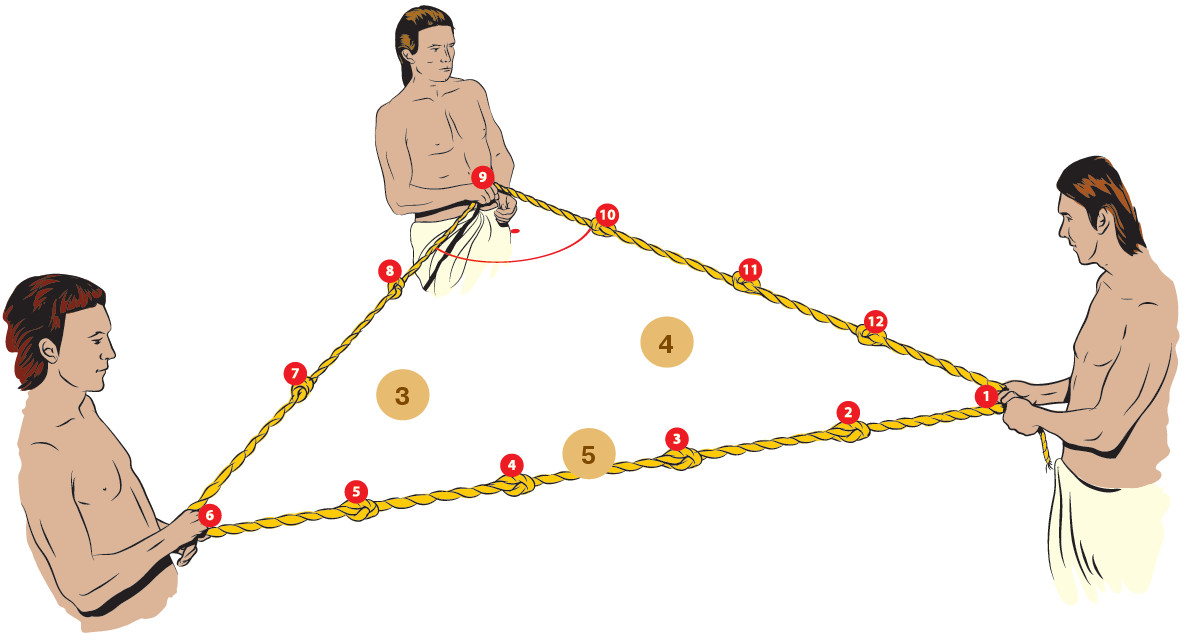
Теорема Пифагора, как известно, гласит: сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы. Прямоугольный треугольник с катетами 3 и 4 и гипотенузой 5 известен с давних времён. Ещё в Древнем Египте строители пирамид использовали для построения прямых углов верёвку с узлами, которые делили её на 12 равных частей. Задача о том, существуют ли другие тройки натуральных чисел, в которых квадрат одного числа равен сумме квадратов двух других, интересовала математиков и в Египте, и в Вавилоне, и в Греции. Сейчас такие тройки принято называть пифагоровыми, разумеется, в честь теоремы Пифагора (древнегреческий математик жил с 570 по 495 год до н. э.), но известны они были задолго до него. Глиняная табличка, содержащая 15 пифагоровых троек, которую археологии называют Plimpton 322, была изготовлена примерно в 1800 году до н. э.
Существует ли бесконечно много пифагоровых троек или их число конечно? Ответить на этот вопрос не сложно. Посмотрим на равенство A2 + (2A + 1) = = (A + 1)2. Если число 2А+1 окажется квадратом (а это может быть любой нечётный квадрат), то мы будем иметь пифагорову тройку. Так получаются равенства 122 + 52 = 132 и 242 + 72 = 252 и, понятное дело, бесконечно много других.
